Turning a convex partition into a Voronoi diagram
 [New wiki page on Voronoi diagrams]
[New wiki page on Voronoi diagrams]A Voronoi diagram (named after Russian mathematician Georgy Voronoi, 1868-1908) is a partition of space based on a set of points. This is the main idea: we are given a set - usually small and sparse - of points which we'll call Voronoi centers. Let's suppose that each of these center points has its own color. Then we can color all of space by coloring any point according to the center it is closest to.
In the figure here (from wikipedia), each black dot is a Voronoi center, and the cells are colored accordingly.
It's easy to think of some places where we might see similar patterns in nature. For example, the shapes on a turtle's shell, or the hexagons of a honeycomb resemble Voronoi diagrams. Close-packed living cells sometimes do as well, maybe because as they became further squished together, their boundaries approached a shape optimized for packing.

You might notice that every cell in a Voronoi diagram is convex - it is a shape without "dents" - every line between two points in a Voronoi cell is contained within that cell (contrast this with, say, pac man). So every Voronoi diagram is a convex partition. Is every convex partition also a Voronoi diagram? No! In fact, there are many ways to draw a convex partition which is impossible to represent as a Voronoi diagram (see the wiki for some details).
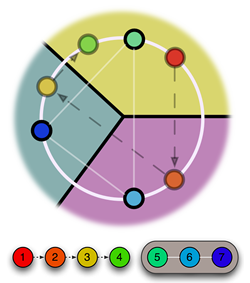
But for those convex partitions which allow a Voronoi diagram, how hard is it to find the corresponding center points? With the right algorithm, it's not so difficult. Here's the main idea: draw a circle around some intersection of three boundaries in the convex partition, pick a random point, and reflect it around the boundaries. After reflecting three times, take the average of this point, and the starting point, along the circle. What you get is a working Voronoi center for that intersection. Reflect this point around to find the other two centers (if you reflect it three times, you'll just get back to your original point). Check out the figure.
Once we have candidate Voronoi centers for any two adjacent 3-intersections, you can expand the circles on which these centers exist until the centers line up. These centers are guaranteed to be the correct unique center for their cells (assuming that the convex partition is a Voronoi diagram). From here, just reflect the centers over the neighboring boundaries of the partition to find all other centers.
This is just a quick summary of a few of the thoughts on the wiki page.


33 Comments:
Nice brief and this fill someone in on helped me alot in my college assignement. Say thank you you for your information.
I dont know what to say. It is undoubtedly one of many superior blogs Ive understand. Youre so insightful, have much genuine stuff to bring towards table. I wish that far more persons study this and get what I got from it: chills. Good career and fantastic blog. I cant wait to study more, retain them comin!
Just saying thanks will not just be sufficient, for the tremendous lucidity in your writing. I will right away grab your rss feed to stay abreast of any updates.
Hey…thanks for that. Fantastic content. I’ll be coming back soon for more news. Cheers!
Nice work Brian you obviously put a lot of work into it. Lets hope 2010 is as fruitful for you.
Brilliant blog post, lots of helpful knowledge.
Best article, lots of intersting things to digest. Very informative
It is simple to see that you are very informed about your writing. Looking forward to future posts.Thank you.
I love it! Could perhaps be a tad more polished, but it’s far better than what we use at the moment, nonetheless
Hey…thanks for that. Fantastic content. I’ll be coming back soon for more news. Cheers!
Looks awesome! I do welcome the tabs placed on the top!
I just cant stop reading this. Its so cool, so full of information that I just didnt know. Im glad to see that people are actually writing about this issue in such a smart way, showing us all different sides to it. Youre a great blogger. Please keep it up. I cant wait to read whats next.
Amazing, totally awesome. I am just getting into writing articles myself, nothing remotely close to your writing potential (ha!) but I'd love for you to take my stuff someday!
[url=http://www.pascherdoudounesenligne.fr]Canada Goose Langford Parka[/url] Senthil - Ganesh produce this film under the banner of Annamali Films (P) Ltd. [url=http://www.pandoraonilnestore.co.uk]cheap pandora charms[/url]
[url=http://www.canadagoosedame.eu]canada goose jakker[/url] dinkczmi
http://www.franceuggboots.eu [url=http://www.franceuggboots.eu]ugg sarenza[/url]
+- buy generic cialis in usa
-- [url=http://buycialisonlinetoday.com/#twww.blogger.com] buy cialis online usa
[/url] http://buycialisonlinetoday.com/#29511 -- cialis online
http://louboutinshop.co.uk In order to increase profits many colonies had to deal with direct trade from Africa.. http://dkgoose.com Eumzayccb http://canadagoosesweden.com
gjmeyw 352404 [url=http://www.canadagoosestorontofactory.ca]canadian goos[/url] 503748 [url=http://www.officialcanadagooseparkas.ca]canada goose in toronto[/url]
When you evaluate the purpose of the saying really like, not only in relations to a romantic connection having a different, although to be a emotion that is certainly engendered when you have miltchmonkey the best romantic relationship yourself far too -- and even to be a experience of higher oneness with the fam and also humankind ( blank ) the idea turns into a lot more crystal clear that each anyone is looking for in life is certainly appreciate.
[url=http://cialisnowdirect.com/#qxzhy]cheap cialis online[/url] - cheap cialis online , http://cialisnowdirect.com/#drssh cialis 10 mg
[url=http://loansheredirectly.com/#omdrd]bad credit payday loans[/url] - payday loans online , http://loansheredirectly.com/#hddhi payday loans online
[url=http://buycialispremiumpharmacy.com/#msntx]buy cialis online[/url] - buy cialis online , http://buycialispremiumpharmacy.com/#vxnxp buy cialis online
[url=http://buyviagrapremiumpharmacy.com/#tdtsg]buy viagra[/url] - viagra online , http://buyviagrapremiumpharmacy.com/#kiwua buy cheap viagra
[url=http://viagraboutiqueone.com/#lbjno]viagra 200 mg[/url] - generic viagra , http://viagraboutiqueone.com/#pyxrt cheap viagra online
[url=http://buyonlineaccutanenow.com/#fitgu]buy accutane online[/url] - generic accutane , http://buyonlineaccutanenow.com/#stcyb cheap accutane online
[url=http://buyonlineaccutanenow.com/#ouvig]buy generic accutane[/url] - cheap generic accutane , http://buyonlineaccutanenow.com/#xifwr accutane online
[url=http://buyonlineaccutaneone.com/#klafd]accutane 5 mg[/url] - buy cheap accutane , http://buyonlineaccutaneone.com/#xpvay accutane online
[url=http://buynolvadexonlineone.com/#xmypc]nolvadex online[/url] - nolvadex online , http://buynolvadexonlineone.com/#akjxe order nolvadex
Đây là những nội dung đáng chú ý trong dự thảo quyết định của Thủ tướng về công bố biểu cước chuyen hang di Ha Noi từ khu công nghiệp, biểu giá dịch vụ vận tải Huế mà Bộ Giao thông Vận tải đang lấy ý kiến. Giải pháp được đưa vận chuyển Đà Nẵng ra nhằm giải quyết các bất cập về việc chủ tàu nước ngoài tự ý thu nhiều phụ phí, gây thiệt hại cho các doanh nghiệp xuất nhập khẩu.
Theo Bộ Giao thông hiện nay các chủ tàu nước ngoài hoạt động đang tự đặt ra nhiều loại phụ cước chuyen hang den Sai Gon mà không được đăng ký, như phụ cước dịch vụ container, phụ cước tắc nghẽn hàng hoá tại cảng, cước mất cân đối container giữa hai đầu bến, cước chuyển phát nhanh Quốc tế ...
phim xác sống phần 6 tập cuốiSeason 6 hứa hẹn sẽ là một mùa phim cực kì bùng nổ, kịch tính và hấp dẫn. xem phim hoàng đế lưu manhBộ phim phản ánh những thông điệp rằng mọi người có thể chia sẻ những khó khăn nhưng không thể chia sẻ sự giàu có xem phim dao ha luu tinh tvbquyết định điều tra và trả thù cho cha tôi là cái Lỗ Cường phát triển bắt đầu kế hoạch của hắn phim ngoa ho tang long 2 tap cuoiNhưng trớ trêu thay, chỉ đến khi vừa mới bắt tay thực hiện Ngày nảy ngày nay, xem phim cong cong xuat cungnhững vị công công này cam chịu kiếp sống nô tài chỉ để được yên bình phim kieu hungmột tác phẩm truyền hình do đạo diễn Vương Tâm Ủy phụ trách sản xuất với kinh phí đầu tư lớn từ TVB phim cuong thi tvb tap cuoi chuyên đi trừng trị những tên tội phạm, những kẻ ỷ mạnh ức hiếp người yếu, trừ gian diệt bạo xem phim Naruto Shippuuden tron bo Họ e sợ một ngày nào đó khi phong ấn không thể kìm giữ được Cửu vĩ hồ, Naruto sẽ trở thành sự hủy diệt cho ngôi làng xem phim One Piece tron bo Cậu theo dấu chân của vị vua hải tặc quá cố, Gol D. Roger, chu du từ đảo này sang đảo khác để đến với kho báu vĩ đại One Piece. phim cam do nghiet nga tap cuoi Bộ phim là câu chuyện về một người phụ nữ buộc phải dấn thân vào thế giới hào nhoáng
Giám đốc đảm đương Nghiên cứu CBRE tại Singapore và khu vực Đông Nam Á, Desmond Sim nhận định: “Hiện vẫn còn đa dạng rào cản và tránh chuyen hang di Bac Kan mà các nước trong khối ASEAN cần phải vượt qua”. đầu tiên là khả năng quản lý yếu kém của cong ty van chuyen di Thanh Hoa, nguồn cung tấp nập với thể dẫn đến biến động giá thuê mặt bằng dich vu van tai hang hoa Bac Giang. Điều này sẽ gây bê trễ hoặc thậm chí ngăn cản việc mở rộng của các nhà bán buôn.
Thứ hai là việc thiếu nguồn lao động có tay nghề cao cũng là thách thức, sở hữu thể gây chướng ngại trong việc van tai hang ra Ha Noi, vận tải hàng hoá Bắc Ninh, chành xe đi Cao Bằng, dịch vụ vận chuyển đi Điện Biên Phủ và mở rộng của các nhà sản xuất công nghiệp mang giá trị cao.
Thứ ba là sự chênh lệch to về chuyên môn giữa các nước thành viên cũng hạn chế những ảnh hưởng hăng hái của đề nghị tự do hóa lao động ASEAN.
Cảm ơn bạn nhiều nhé.
This comment has been removed by the author.
Finland has maintained its embassies in How To Apply For South Africa Visa From India, its famously known consulates in Bangalore, Kolkata and in Mumbai.
lockout service, install and repair of locks, key duplication and creation, auto smart key duplication and more and For more information please click this now locksmith near me locksmith in fort worth tx.
The next time I read a blog, I hope that it does not fail me just as much as this particular technology one. I mean, I know it was my choice to read, nonetheless I actually believed you would probably have something useful to talk about. All I hear is a bunch of whining about something you could fix if you were not too busy looking for attention.
Post a Comment
<< Home